1. 베르누이 방정식
에너지 보존 법칙을 적용하면 유체의 압력, 높이, 흐름 속도 사이의 관계가 도출됩니다. 이 관계를 베르누이 방정식이라고 합니다. 유체 역학에서 가장 잘 알려지고 널리 사용되는 방정식 중 하나입니다.
베르누이의 방정식은 흐르는 유체에 대한 에너지 보존 법칙으로 볼 수 있습니다.
운동 에너지 = 운동에너지 +위치에너지 (W𝑜𝑟𝑘 𝑑𝑜𝑛𝑒 = 𝐾𝑖𝑛𝑒𝑡𝑖𝑐 𝐸𝑛𝑒𝑟𝑔𝑦 +𝑃𝑜𝑡𝑒𝑛𝑡𝑖𝑎𝑙 𝐸𝑛𝑒𝑟𝑔𝑦)
∆𝑊=∆(𝐾𝐸+𝑃𝐸)
일은 힘에 거리 곱한 것과 같습니다:
𝑊=𝐹𝑑
여기서 압력과 힘을 연결하는 공식을 대입할 수 있으며, 이는 다음과 같습니다:
𝑊=𝑝𝐴𝑑 (여기서 A는 면적을 나타냅니다.)
부피는 면적과 높이(거리)를 곱하여 구합니다. 따라서:
𝑊=𝑝𝑉
일은 다음과 같습니다:
∆𝑊=𝑝1𝑉1−𝑝2𝑉2
운동 에너지는 움직이는 질량의 에너지입니다:
K𝐸 =𝑚𝑣2/2 =𝜌𝑉𝑣2/2 (여기서 V는 부피를 나타냅니다.)
잠재 에너지는 높이에 의존합니다:
P𝐸 =𝑚𝑔𝑦=𝜌𝑉𝑔𝑦 (여기서 y는 높이를 나타냅니다.)
대입하면........

V로 나누기:

같은 지점을 가리키는 용어를 방정식의 같은 쪽에 배치하기 위해 공식을 재배열하면 다음과 같습니다.
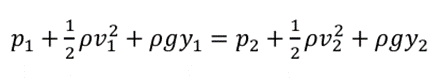
베르누이 방정식에는 몇 가지 제한이 있습니다::
- 정상 흐름
- 비압축성 흐름 (즉, 밀도가 일정함을 의미)
- 마찰 없는 흐름
- 유선에 따라 흐름
실제 상황에서는 확장된 베르누이 방정식을 사용하여 문제를 분석할 수 있습니다:
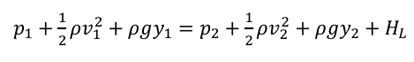
- HL – 마찰 또는 점성으로 인한 머리 손실.
- y1과 y2 – 입구와 출구의 높이
2. 유동의 종류 (Types of flow)
세 가지 유동 영역이 있습니다. 유동이 안정된 상태로 흐를 때 이를 유선 유동(be streamline) 또는 층류 유동(laminar flow) 이라고 합니다. 이는 유동이 진행됨에 따라 유체의 다양한 축 방향 층이 그대로 유지되기 때문입니다. 소위 난류 유동(turbulent flow)은 불규칙한 유동입니다. 이는 유동관의 층들이 그대로 유지되지 않고 난류, 즉 유동의 불규칙한 움직임으로 인해 끊임없이 혼합되기 때문입니다. 전이 유동(Transitional flow )은 층류와 난류가 혼합된 유동입니다.
2-1. 층류 흐름(Laminar flow)
층류는 매끄러운 유선과 고도로 정렬된 운동이 특징입니다. 파이프가 입구 길이에 비해 충분히 길면 입구 효과는 무시할 수 있으므로 유동은 완전히 발달합니다. 층류는 유체가 섞이지 않고 평행한 층으로 흐를 때 발생합니다. 유체의 속도는 어느 순간에도 일정합니다. 유동이 정상 상태이므로 가속도는 없습니다. 레이놀즈 수가 2300 미만인 원통형 파이프의 유동은 층류입니다.
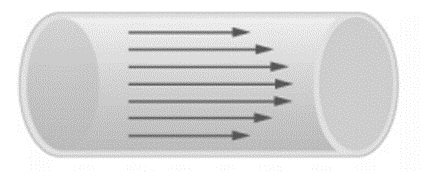
다음 방정식은 하겐-푸아졸 방정식(Hagen-Poiseuille’s)이라고 하며, 비압축성 유체의 지속적 층류 흐름에서의 수두 손실 계산에 사용됩니다.

- HL = 헤드 손실 (m)
- p = 압력 (Pa)
- ρ = 밀도 (kg/m3)
- g = 중력 가속도 (g = 9.81 m/s2)
2-2. 난류 유동 (Turbulent flow)
난류는 속도 변동과 매우 무질서한 운동이 특징입니다. 실제로 접하는 대부분의 유동은 난류입니다. 난류는 액체의 흐름선이 불규칙하고 시간이 지남에 따라 변화할 때 발생합니다. 유체 흐름의 경로도 불규칙하며 미세한 와류 지역을 형성합니다. 흐름은 레이놀즈 수가 4000을 초과할 때 난류입니다. 실제로 공학에서 대부분의 흐름은 난류입니다. 그러나 난류 흐름의 이론은 이 흐름이 변동에 의해 지배되는 매우 복잡한 메커니즘이기 때문에 아직 개발이 덜 되었습니다. 따라서 난류 흐름은 실험적인 측정을 적용하여 분석됩니다.

난류에서 소용돌이와 여파는 흐름을 예측할 수 없게 만듭니다. 아래의 공식은 다르시 방정식이라고 하며, 완전히 발달된 흐름의 계산에 사용됩니다.

- f = 파이프 내부의 거칠기와 관련된 마찰 계수
- L = 파이프의 길이 (m)
- D = 파이프의 내부 직경 (m)
- Vavg = 평균 유체 속도 (m/s)
- g = 중력 가속도 (g = 9.81 m/s²)
2-3. 전이 유동 (Transitional flow)
류에서 난류로의 전이는 갑작스럽게 일어나지 않습니다. 파이프 중앙에서는 난류가, 가장자리 근처에서는 층류가 발생하는 특정 영역에서 발생합니다. 이 흐름은 완전히 난류가 되기 전에 층류와 난류 사이를 오갑니다. 레이놀즈 수가 2300에서 4000 사이일 때 전이 흐름으로 간주됩니다.
3. 레이놀즈 수 (Reynolds number)
레이놀즈 수는 유동이 층류인지 난류인지를 나타낼 수 있습니다. 층류에서 난류로의 전이는 표면 거칠기, 유속, 형상, 표면 온도, 유체 종류 등에 따라 달라집니다. 유동 영역은 주로 유체 내 관성력과 점성력의 비율에 따라 결정됩니다. 이 비율을 레이놀즈 수라고 하며, 다음과 같이 표현됩니다.
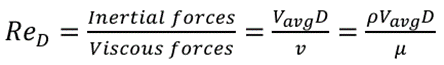
- ReD = 원통형 파이프의 레이놀즈 수. 레이놀즈 수는 무차원 수이다.
- Vavg = 평균 유속 (m/s) - average flow velocity
- D = 지름 (m) - diameter
- v = 유체의 운동 점도 (m2/s) - kinematic viscosity of the fluid
- µ = 동점도 (Pa·s) - dynamic viscosity
임계 레이놀즈 수 Recr는 유동이 난류로 변하는 지점의 수치입니다. 이 숫자의 값은 다양한 형상과 유동 조건에 따라 다릅니다. 원형 파이프 내부 유동에 대한 일반적으로 인정된 임계 레이놀즈 수의 값은 Recr = 2300입니다.
- Re ≤ 2300일 때는 층류
- 2300 ≤ Re ≤ 4000일 때는 전이 흐름
- Re ≥ 4000일 때는 난류
'설계자료' 카테고리의 다른 글
| 나사(screw) 나사 제도법 2 - 규격 표 (0) | 2025.05.02 |
|---|---|
| 열전도률 - Thermal Conductivity (0) | 2025.05.01 |
| 기하 공차 - Geometric Dimensioning and Tolerancing (0) | 2025.04.30 |
| 영문 표기 - 기계 가공 영문 표기 및 약어 (2) | 2025.04.25 |
| 모터 감속기 선정 자료 (0) | 2025.03.28 |



